(公開日:2020年5月19日)
これまでの授業で実際に体験していただいたように,私たちの眼がカメラに似ているといっても,何かものを「知覚する」という段階では,人は,カメラのように外界の光景を忠実に写し取っているわけではないようですね。このことをもっとも端的にあらわす現象が「錯覚」です。
「錯覚」(illusion)とは,私たちの知覚した結果が実際の対象の物理的特性とは異なることを言います。一般的な用語として錯覚という言葉を使うときには,見間違いという意味で使うこともありますが,心理学において問題となる錯覚は「正常な現象」です。したがって,錯覚量の違いはあっても,いつ見ても,何度見ても,誰が見ても,同じような錯覚が生じます。
このような錯覚を研究することによって,人の脳の中で行われている情報処理の仕組みを解明する手がかりが得られると期待され,知覚心理学の領域では古くからたくさんの研究が行われてきました。視覚における錯覚は,「錯視」(visual illusionあるいはoptical illusion)と呼ばれ,特にたくさんの研究が行われています。
錯視には,広義(広い意味)にとらえると,幾何学的錯視,多義図形,逆理図形,主観的輪郭,明るさの対比,仮現運動の知覚など,多種多様な現象が含まれるのですが,その中でも図形の幾何学的性質(長さや,面積,方向,角度,曲線など)が実際とは異なって知覚される現象は「幾何学的錯視」と呼ばれ,たくさんの図形が知られています。
この幾何学的錯視図形を紹介する前に ,まずそれ以外のもので知っておいていただきたい錯覚的知覚現象をいくつか紹介します。前述したように,これらも広い意味では錯視現象に含めて紹介されることがしばしばです。
なお,今回の授業で特に引用元(リンク先)のない図は,吉田(2006)や吉田(2011)で使用したものです。
多義図形
下の図は,前回,「図と地」のお話をするのにお示ししたルビンの杯です。もっとも有名な多義図形のひとつですね。図の白い部分に注意を向けると優勝カップのような杯が,黒い部分に注意を向けると向かい合った人の横顔が見えます。「多義」とは「多くの意味」という意味ですが,このように二つの図形が入れ替わる図形は「両義図形」あるいは「反転図形」と呼ばれることもあります。多義図形でネットを検索すると他にも有名な図形を見つけることができると思います(「老婆と若妻」,「アヒルとウサギ」などいろいろあるのですが,検索結果の中のどれかわかりますか? ^^)

逆理図形
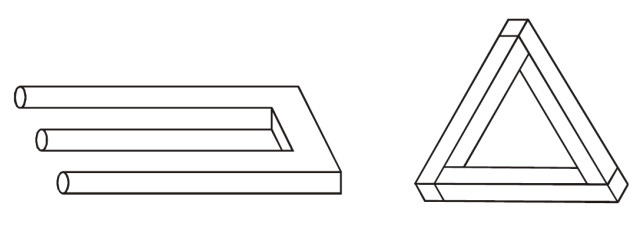
「逆理図形」とは「理に逆らった」図形という意味で,「ありそうに見えるけれども,実際には存在しえない形」です。「矛盾図形」あるいは「不可能図形」と呼ばれることもあります。下の図は代表的な逆理図形の例です。前回も紹介した芸術家,エッシャー(←検索リンク)はこのような存在しえない構造物に関する作品もたくさん残していて有名ですので,みなさんもご覧になったことがあるのではないでしょうか。
主観的輪郭
大学で心理学を勉強するようになると,いろいろな授業で「主観的」(subjective)あるいは「客観的」(objective)という言葉を聞く機会が増えます。「心理学研究法A」を履修している人には,データを支える三本の柱として「妥当性・信頼性・客観性」の概念を説明しましたが,客観とは「第三者の視点で物事をみたり考えたりする」ことです。となると,その逆の主観は,「自分という存在を中心とした物事の見方」ですね。主観的輪郭とは,主観,つまり自分の中で作られる輪郭です。下の図が代表的な図です。カニッツァ(Kaniza, G.)という陽気なイタリアンの心理学者が多くの研究を行ったので,このような図を「カニッツァの三角形」と呼ぶこともあります。

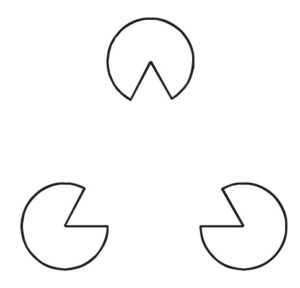
上の図では,欠けた円形が3つ向かい合っていますが,その欠けた部分が一直線になるように描かれていると,私たちは,3匹のパックマン(←1970年代のゲームのキャラ)が向かい合っているようには見えず,3つの黒い円の上に白い三角形が横たわっているように見えます。その三角形は,背景の白よりもひときわ白く見えて,存在しないはずの輪郭さえくっきりと知覚されます。これが主観的輪郭です。
これに対して,下の図ではいかがでしょうか。下の図ではパックマンが輪郭画で描かれています。すると,主観的輪郭は見られなくなったのではないでしょうか。輪郭画にすると,脳はこれがパックマンの形であるという見方しかしなくなります。それに対して,上の図のように黒塗りのパックマンが向かい合っていると,脳は,「本当は真円が3つあるのだけれども,その上に白い三角形が乗っかっているので,結果としてパックマンのように見えているんだ」と解釈するのです。それが幻の三角形が見える原因だと考えられています。
明るさの対比
ものの明るさや色は,周囲との関係でより鮮やかに見えることがあります。明るさの対比とは,同じ灰色でも,黒い背景の上では明るく,白い背景の上では暗く感じられる現象です。まず,下の図を見てください。白と黒の背景の上に灰色のリングを置いてみました。…が,この灰色のリングの明るさが背景によって変わることはありません。なぜだと思いますか? 今の状態では,リングがつながっているので,脳はそれを1つの対象物だと認識しているからです。

では,下の2つの図ではどうでしょうか。今度は,灰色のリングに対して,白黒の境目のところで線分を入れたり,上下にずらしたりして,分断してみました。すると,脳は,左右半分ずつのリングを別の対象物だと認識するので対比効果を起こして,同じ灰色なのに白の背景の上では暗く,黒の背景の上では明るく見えるようになったのではないでしょうか。

このように錯覚といっても,単純にこういう図形だとこんな風に錯覚が生じるというような単純なものではなく,脳が,見えるパターンをどのように解釈しているかの影響を大きく受けるところが,研究対象として興味深いところです。
下の図はその一例です。この図は,マサチューセッツ工科大学(MIT)のエーデルソン(Adelson, E. H.)が示した「チェッカー・シャドウ錯視」と呼ばれる有名な明るさ錯視です。この図において,チェッカーボード上のAとBの領域は同じ明るさで描かれているのですが,同じに見えますか? 私たちには二つの領域はまったく異なる明るさに知覚されますよね(Aの方がずっと暗いですよね)。私たちの脳は,眼の網膜に届いた光の量だけで明るさを知覚しているわけではありません。脳は,Aの領域には光があたっていて,Bの領域には影が差していることも評価します。この仕組みによって,私たちは,照明に依存しない対象の表面の明るさを知覚できるようになっているのです。

Adelson’s Checker-Shadow Illusion

アニメーションを作ってみましたが,どうでしょうか。
幾何学的錯視
それでは,今日の主役の幾何学的錯視についてご紹介します。数学に,図形や空間の性質について研究する「幾何学」という分野がありますが,幾何学的錯視はこの幾何学が研究対象とするような,図形の長さや面積,方向,角度,曲線などが実際とは異なって知覚される現象です。ただ,最近はたくさんの錯視が知られるようになっていて,みなさんの中にもいろいろと知っている人がいらっしゃると思いますが,今日,ここで紹介するものは「地味」な(←ちょっとつまらない)ものばかりです。すみません (^^;)。この授業は専門概論ですので,取り上げる錯視図形は,心理学の歴史において著名な図形です。心理学を勉強した学生なら,名前くらいは知っておいてほしい図形というわけですね。
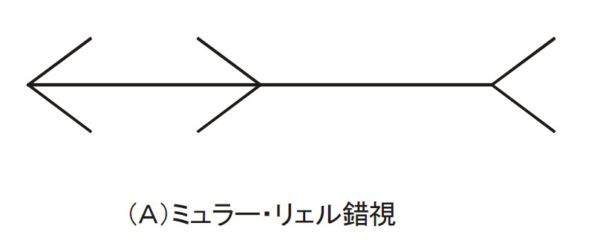
まず,下の図は「ミュラー・リェル錯視」です。左右の水平線分の長さは同じなのですが,矢羽根状の斜線が内向きにつくと短く,外向きにつくと長く見える錯覚が生じます。錯視量が非常に大きいことで有名な錯視です(心理学を学ぶ全国の大学生の多くが,最初の心理学実験の題材として勉強することでも有名です ^^)。
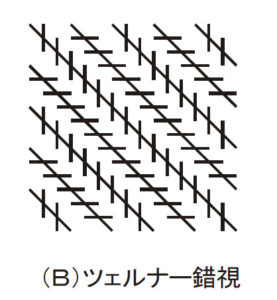
次の図は「ツェルナー錯視」です。上のミュラー・リェル錯視が長さが変わって見える錯視であるのに対して,こちらは角度の錯覚をもたらす有名な図形です。平行に描かれた線分に,斜めの短い線分を重ねて書くと,あら不思議,平行だった線分が平行には見えなくなってしまいます。
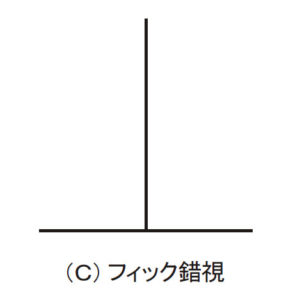
次の錯視図は「フィック錯視」です。「垂直-水平錯視」と呼ばれることもあります。錯視図形というのは,一般的に「主線」と呼ばれる,長さや角度が錯覚によって影響される部分と,「条件線」と呼ばれる,主線に影響を及ぼす部分に分かれるのですが,この図形は,主線を2本組み合わせただけという,おそらく一番単純な構造でありながら,大変大きな錯視量をもちます。下の図において,逆T字型に組み合わされた水平線分と垂直線分はまったく同じ長さなのに,同じに見えません。
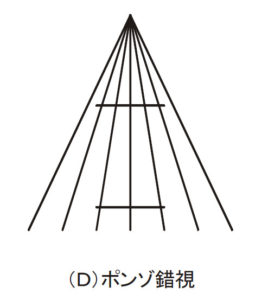
下の図は「ポンゾ錯視」です。放射状に広がる斜線の中に2本の同じ長さの水平線分が描かれていますが,上の方が長く,下の方が短く見えるのではないでしょうか。私たちは,このような放射状の線分に奥行き感を感じるので,後で述べる奥行理論による錯視の説明に使われることでも有名な錯視図です。
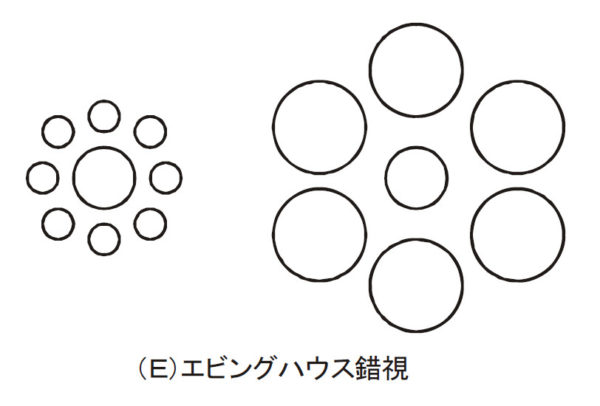
次の図形の名前になっているエビングハウス(Ebbinghaus, H.)は,世界で最初に記憶の忘却に関する実験的研究を行った研究者として有名な人物です。前の方で明るさの対比の話をしましたが,この「エビングハウス錯視」は,大きさの対比によって生じる錯視です。左右の中央にあるのは同じ大きさの円ですが,小さな円で囲まれたものは大きく,大きな円で囲まれたものは小さく見えます。
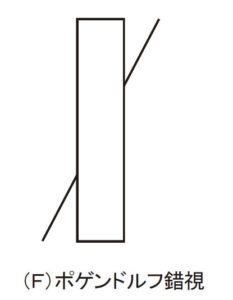
次は「ポゲンドルフ錯視」です。斜めにくっついている右上と左下の線分は一直線になるように描かれているのですが,我々にはそれらがずれているように知覚されます。嘘だと思った方は,物差しをあててみてください (^^)。
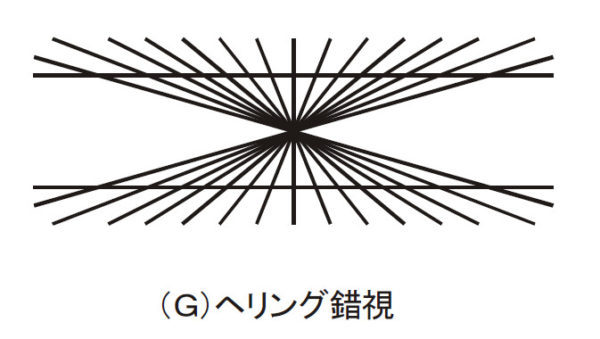
この後の2つの図形に見られる錯視は同じ仕組みで生じていて,それは角度の錯覚が起きる仕組みのヒントを与えてくれます。まず最初に示すのは「へリング錯視」です。放射状の線分の中に2本の平行な直線が引かれていますが,その直線が真ん中で膨らんでいるように見えませんか?
次の錯視は心理の学生さんならもう知っている心理学の祖であるヴントが報告した「ヴント錯視」です。上のヘリング錯視とは逆に,こちらは2本の平行線分が真ん中ですぼまって見えますね。
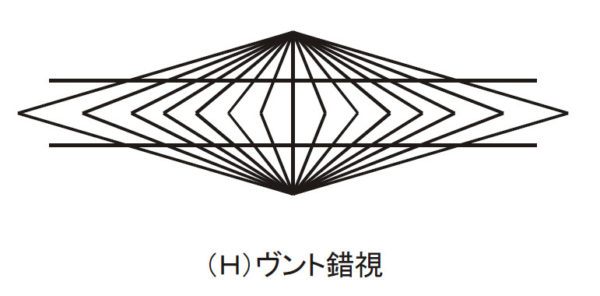
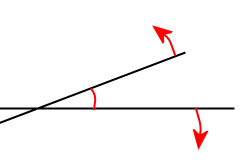
上の2つの図をご覧になって,放射線の拡散する方向が逆になると曲がり方が逆になるのねと思った人は多いと思います。実は,線分同士が斜めに交わるとき,そこに鋭角(90度未満の尖った交わり)が生じますよね。ヘリング錯視もヴント錯視も,この鋭角が直角方向(90度側)に開くように線分が曲がっているのがわかるでしょうか。
下の図に描いたように,図形に鋭角が存在すると,私たちの脳は,それをより直角に近い方に広げて錯覚する性質があるようなのです。このような傾向を「鋭角過大視」といいます。
となると,他の錯視図も,角度の錯覚は鋭角過大視で説明できる方向に錯視が生じているのがわかるでしょうか。ツェルナー錯視では斜めの線分が交わることによって平行線が平行でなくなりましたが,その錯視は斜めの線分との交点が直交する側に生じています。ポゲンドルフ錯視についても,鋭角を過大視する傾向があるとすれば右上の線が左下の線の上側を走るように錯覚されることに納得がいくでしょう(ポゲンドルフ錯視の生起因については他にも諸説ありますが)。
なぜ錯視が生じるのか
さて,角度についてはなぜ錯視が生じるのかがわかったような気がしますが,それだけではミュラー・リェル錯視やポンゾ錯視,フィック錯視のような長さの錯視が生じる原因はわかりません。
錯視図形の多くは,19世紀後半から20世紀前半にかけて発見されたので,現在に至るまで研究の歴史は長く,研究の数も膨大なのですが,なぜ錯視が生じるのかという生起メカニズムについては,まだ統一的な理論は見つかっていません。しかし,いくつかの図形については,奥行き知覚との関連で錯視が生じるメカニズムの説明が行われることがあります。それを紹介しましょう。
下の写真は,グレゴリー(Gregory, R. L.)という研究者によるポンゾ錯視の説明について,授業で話をするために私が撮った写真です。

遠近感が強調されたハの字型の線路の写真上に描かれた二つの白い帯は,上側が大きく(長く),下側が小さく(短く)見えるでしょう。この写真では,上の帯は線路の遠方の枕木のあたりに,下の帯は手前の枕木のあたりにあるように感じられますね。3次元空間においては,遠くにあるものと近くにあるものが同じ大きさで目に映るならば,遠くのものの方が大きく,近くのものは小さいはずです。脳はこの知識をもっていると考えられます。これがハの字パターンに描かれた2本の水平線に錯視が生じる原因の一つではないかと考えられます。
ポンゾ錯視のように明らかに奥行きを感じる図形でなくても,同じようなパターンが実際の3次元空間に見られることもあります。下の写真は,フィック錯視の逆 T 字型のパターンが見られる例です(7号館のセミナー室で撮影しました)。わかりますか? この写真で,2つのテーブルによって作られる逆T字の垂直線と水平線はまったく同じ長さです(あくまでも2次元的に)。しかし,この例でも,フィック錯視と同じように,二つのテーブルで作られた縦の線は,下側の横の線よりもずいぶん長く知覚されます。

これらの図形に共通することは,平面図形の幾何学的特性を認識する上では誤った知覚であっても,それを奥行きパターンとしてとらえるならば,3次元的には正しい知覚をしていると考えられる点です(実際にセミナー室のテーブルは,長辺が短辺の2倍以上の長さをもっています)。3次元の世界に適応するために発達した私たちの知覚システムは,2次元の幾何学構造よりも,3次元の広がりを認識することを重視しているのかもしれません。
3次元空間における錯視
3次元空間の中でも錯視が生じることがあります。上のポンゾ錯視の例のように,特に,奥行きを誤って知覚すると,それは大きさの錯覚をもたらします。その代表的な事例が,「エイムズの部屋」と呼ばれる錯覚です。下の写真はその模型です(この模型の設計図は私のホームページで公開しています)。

エイムズの部屋は歪んだ作りをしていますが,覗き穴(写真では付箋紙を貼った壁の向かい側にあります)を通して見ると,歪みのない四角い部屋に見えるように設計されています。ですから,穴から覗くと,距離が異なる付箋紙を同じ距離にあると脳が錯覚するので,付箋紙が違った大きさに知覚されます。下のビデオは,覗き穴のある壁を取り去って,デジカメでビデオを撮ってみましたが,錯覚が起きる様子がわかるでしょうか。
他にも,日常の3次元空間で生じる錯視として,「月の錯視」がよく知られます。地平線近くにある月は,天空にある月よりもはるかに大きく見えるので,それを錯覚と思わない人もいるくらいです。しかし,月の物理的な大きさは視角にして約0.5度なので,腕を伸ばして見た5円玉や50円玉の穴と同じ大きさです。だから,地平線上で大きな月を見る機会があったら,5円玉を出して,その穴に入れて見てみましょう。穴に入ったとたんに,小さな月になりますよ (^^)。
大きく見える地平の月を写真に撮ってがっかりした経験を持つ人もいるでしょう。下の写真は,とても大きく見える月の出を,写真に撮ったものですが,そこに写っているのは物理的な大きさの小さな光の点であって,感動的に大きく見えた月ではありません。そうです,月の錯視は写真には写らないのです。

テレビやインターネットなど,メディアが発達した現代社会において,私たちは様々な事柄について実体験によってではなく間接的に見て知ることができます。しかしながら,実体験で得られるもののすべてがメディアに映るのではないということを知っておくべきだと思います。例えば,私たちには,空や海の青は実際よりも青く,木々の緑も実際よりも鮮やかに見えます(「記憶色」と言います)。これも心を通して見ているから起きる現象です。実際に,空や海,木々などを写真に撮って,思ったよりも色が鮮やかでなくてガッカリした経験をもつ人も多いと思います。たとえそれが錯覚であっても,実際に体験することのもたらす感動は大切なのですよ。それは写真などのメディアには写らないのです。
最後に
ここまで話をしてきて,月の錯視について,ひとつ問題を提起します。私たちの知覚とカメラ,どちらが正確で,どちらが錯覚という誤りを犯しているのでしょうか? 月の「錯視」というくらいだから,私たちの知覚が錯覚を犯していると考えるべきですよね…と思って,授業でも私は学生さんたちに大きな月は錯覚だと教えていました。
でも,この考えを改めた方がいいと思う出来事に直面したのです。それが,2014年の8月に広島で起きた下の土砂災害です。この災害現場を実際に見たとき,その規模の巨大さに震えました。そこにあった「山」が流れ落ちてなくなっているという感覚なのです。しかしながら,知覚心理学者として気づいたのが,その災害の「巨大さ」が写真には写っていないということです。

その時,これは月の錯視と同じだなと思いました。
その後,私のゼミに入った学生さんに,錯視の研究をしたいという人がいたので、「じゃぁ、月の錯視の研究をしようよ」と話をして、なんで地平の月は写真に小さく写ってしまうのかを研究しました。
その時の道具として使ったのがバーチャルリアリティ(VR)です。実験では,VR内の仮想の世界に町を作りました,そこに実際と同じように月を置いたのです。そして,その月の大きさを2次元平面であるディスプレイ上で評価する条件と,VRゴーグルを使って実際にその世界に入って評価する条件で,月の錯視が生じるかどうかを調べたのです。その仮想の世界の中を学生がドローンのように飛んで遊んでいるビデオがあったので見てみてください。心理実験のために,道路の先の地平線上とその上に2つの月のある世界を作ったのです。
…で,実験の結果ですが,VRの世界では現実の世界と同じように地平の月は天空の月よりもはるかに大きく見えました。それに対して,写真のように2次元になったディスプレイ上では,月の錯視はほとんど起こりませんでした。
このことは,つまり,VRを使えば,土砂災害などの現場の災害規模の大きさを知覚的に再現して伝えられることを意味します。災害教育にVRが有効に使えることがわかりました。
地平線近くで月が大きく見えるのは錯覚ではないのです。地平線近くでは,建物や山々など,たくさんの地上物が同時に視界に入ります。だから,月という天体の巨大さがわかるのです。それに対して,天空高く昇ってしまうと周囲に比べるものがありません。だから小さく錯覚して見えてしまう。写真もそうです。写真の中には空間の広がりがありません。だから,本来は大きな月も小さく感じてしまうのです。
ちなみに,この研究は日本の心理学における中心的な学会である日本心理学会で発表して学会賞をいただきました。うちの学生の卒論研究を学会でも認めてもらえたので,ちょっとした自慢です (^^)。
錯視のホームページ
「錯覚・錯視」ということで長々と書いてきましたが,錯視に興味がある人がいらっしゃったら,ぜひ立命館大学の北岡明佳先生のホームページを見てみてください。北岡先生は錯視研究の世界的な第一人者ですし,錯視大好き人間なので,とても楽しく研究されていますから,見ていて飽きないくらいたくさんの錯視を紹介していただいています。
ちなみに,下の錯視図は「蛇の回転」と名づけられた「運動錯視」です。大きな画面ほどわかりやすいのですが,静止画なのにうねうねと動いて見えます(スマートフォンの小さな画面では動かないかもしれません)。

ちなみに,下のようなYouTubeビデオも見つけました。このように錯視は人間に限らず,多くの動物でも起こっているようですね。ネコってかわいいですよね。
以上,今日は,錯覚・錯視についてお話ししました。
お疲れさまでした。
出席確認
(今回から,授業に対する意見・感想・質問を記入してもらう形式にします。「特になし」などではなく,必ず自分の意見・感想・質問を書いてください。それを評価対象とします)
参考文献
- 吉田 弘司(2006).感覚・知覚―心のフロントエンド― 羽生義正(監)・中丸澄子・松本一弥・小早川久美子・有馬比呂志(編) 心理学への扉(pp. 58-78) 北大路書房
- 吉田 弘司(2011).周囲のものごとを認識する 今井芳昭(編)心理学から見る日常生活(pp. 115-135) 八千代出版