(公開日:2020年7月8日)
「思考」とは
次の問題について考えてください。
【問題】
今,ここに9枚の金貨があります。その中に1枚だけ,規定の分量の金が使われていない不良品が混ざっていることがわかりました。不良品は他の金貨よりも軽いので,天秤を使って,その不良品を見つけてほしいと頼まれました。ただし,天秤は「2回」しか使うことができません。2回で不良品を見つけるにはどうすればいいでしょうか?

答えはわかりましたか?
答えが見つかったかどうかは別にしても,今,みなさんは「思考」によって,上の問題の答えを見出そうとしました。この,「思考」という過程も「情報処理」の過程であるとみなすことができる点で,知覚や認知と同様に扱うことができます。実際,近年,人工知能の処理能力を大幅に増加させた一因であるディープラーニングの技術は,知覚の過程で行われている情報処理を神経回路モデル(深層神経ネットワーク)としてモデル化したものを計算機上に実装したものです。
余談ですが,ディープラーニングの基本アイデアともなっているコグニトロンというのは日本人研究者の福島邦彦さんが考案したものなのですが,なんと私,学生時代に勉強してたんですよ(↓下の本)。そんなすごい研究だなんて思わずに…これが凡人というものですねぇ (^^;)。

さて,思考も情報処理過程ではあるのですが,通常の知覚・認知過程とは異なり,(1) 利用すべき情報が,考える時点では目の前には存在せず,すべて記憶内の情報を用いることが多い,(2) その情報の操作過程のほとんどについて,私たちは自分自身で意識しながら行っている,(3) 解を得るまでの時間が,知覚・認知に比べてかなり長い(知覚の成立はミリ秒単位であるのに対して,思考における問題解決には分単位の時間がかかる)など,特有の側面ももっています。
そこで,今日は,この思考の過程(プロセス)について,「考えて」みたいと思います (^^)。
上の問題の解
- 9個の金貨から,適当に3個ずつ2グループの金貨を取り出して,それらを天秤に載せます(1回目)。

- 上で,もし天秤がどちらかに傾けば…
- 軽い皿にある3個の金貨のうちの2枚を取り出して天秤に載せます(2回目)。
- 天秤が釣り合えば…皿に乗せなかった金貨が不良品です。
- 天秤が傾けば…軽い方の皿の金貨が不良品です。
- 軽い皿にある3個の金貨のうちの2枚を取り出して天秤に載せます(2回目)。

- もし,最初の3個ずつの天秤が釣り合えば…
- 最初に皿に乗せなかった残りの3枚の金貨の中に不良品が入っているわけなので,そのうちの2枚を取り出して天秤に載せます(2回目)。あとは,上と同じですね (^^)。
- 天秤が釣り合えば…皿に乗せなかった金貨が不良品です。
- 天秤が傾けば…軽い方の皿の金貨が不良品です。
- 最初に皿に乗せなかった残りの3枚の金貨の中に不良品が入っているわけなので,そのうちの2枚を取り出して天秤に載せます(2回目)。あとは,上と同じですね (^^)。
有名な思考問題
思考とはある種の「問題解決」と考えることができますので,人間の思考に関して,これまでに有名な問題が知られています。そこで,まず,それらをいくつか紹介しながら,私たちが行っている思考過程の特性についてみていきたいと思います。上の天秤問題を含めて,これらはすべてとても有名な思考問題なので,(天秤問題の金貨の枚数などいろいろバリエーションはありますが)すでにどこかで聞いたことのある問題だと思いますよ。
9点問題
【問題】
下の9つの点をすべて通るように,一筆書きの4本の線分で結んでください。

できましたでしょうか?
実は,知覚研究で有名なゲシュタルト心理学者たちも,思考の問題を研究しています。彼らは,思考は「再生的思考」と「生産的思考」の2つに分類することができると考えました。再生的思考は,過去に経験した問題解決に基づいた思考方法であって,習慣や行動が再生されることによってなされます。それに対して,生産的思考は,新たな関係性に気づくことであって,この思考方法は人間のもつ 創造性に深く関与していると考えられています。心理学において問題とされる「思考」の多くは,後者(生産的思考)であり,そこで行われる問題解決には,何らかの「洞察」が必要になります。そのため,心理学で研究対象となる問題解決は「洞察的問題解決」と呼ばれることもあります。
上の9点問題では,再生的思考によって解決しようとすると,その問題の構造や過去の経験によって,洞察に必要な関係性の発見が阻害されて,思考が手詰まり(インパス,impasse)に陥ってしまいます。そこで必要とされるのが,問題の再構成化(再構造化)であるといわれます。この問題の再構成化が,新たな関係性を発見することに結びつき,それによってこの問題の解にはじめて到達することができるのですね。
9点問題においても,9つの点の配置による四角い知覚的枠組みと,過去に蓄積された一筆書きの経験の枠組みによって,洞察的問題解決を妨害する心的制約が生じていると考えられるわけです。実際,9点問題の答えがわからない人はすべて,一筆書きの直線を四角い枠の内側だけで引こうとします。このように,思考が要求される問題解決においては,再生的思考によって問題を解決しようとする回答者内部にある思考パターンが,むしろ制約となって,生産的思考(洞察的問題解決)を邪魔してしまうわけですね。
【9点問題の答えの例】

ルーチンスの水がめ問題(Luchins’s water jar problem)
【問題】
容量の違う3つの水がめがあります。Aの容量は21リットル,Bの容量は127リットル,Cの容量は3リットルです。この3つの水がめを使って,「100リットル」の水を測りとるにはどうしたらいいでしょうか?
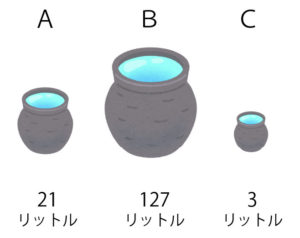
この問題は,洞察よりもむしろ「試行錯誤」によって,解決できるような問題ですね。
- まず,B(127リットル)の水がめを一杯にして…。
- BからA(21リットル)に水を移して…(すると,Bの中身は127 – 21で106リットルになる)。
- Bから今度はC(3リットル)に水を移して…(Bの中身は106 – 3 = 103リットルになる)。
- もう一度,BからC(3リットル)に水を移して…完成!(Bの中身は103 – 3 = 100リットル!)
上でやってもらった問題は,下の表の1番目の問題になります。2番目以降も続けてやってみてください…というのがルーチンスの水がめ問題です。
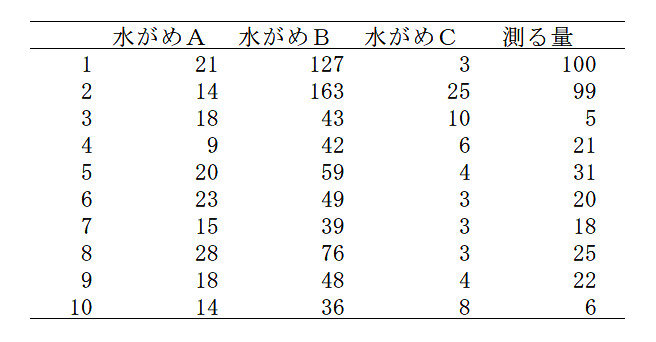
実際に実験室でこの水がめ問題を連続してやってもらうと,最後の10問目が解けない参加者が出てきたり,解けても上の問題よりも時間が長くかかることがみられます。10問目では,下の3つの水がめで「6リットル」を測りとらなければなりません。
-300x223-1.jpg)
この10問目の問題は,上の9つの問題よりもずっと簡単に解くことができるはずの問題です(実際に上の問題を経験していない参加者はあっという間に解いてしまいます)。Bの水がめを使わないで,AとCだけで6リットルを測りとればいいわけですね。
このルーチンスの水がめ問題は,「構え」(set)の固さや固執(固着)を示す例です。「構え」とは,知覚や認知,学習,問題解決などにおいて,主体がもつバイアス(認知の傾向あるいは認知の偏り)です。再生的思考のような問題解決においては,私たちは過去の経験から作った構えによって,問題を認知しやすくして,処理を促進していますが,同じような問題解決を繰り返していると,思考がその問題解決パターンに固着してしまうため,柔軟な問題解決ができなくなってしまうわけですね。
ちなみに,上の水がめ問題で10問目の解き方に気づいても,後半の(第6問以降の)問題がすべてAとCの水がめだけで解けることには気づかない人も多いのです。これも構えの固さの表れですね (^^)。
メイヤーの2本のひも問題(Maier’s two-string problem)
【問題】
あなたは,天井から垂れ下がっている2本のひもを結ばなければなりません。部屋にはイスやプライヤー(ペンチ)などいくつかの物がありますが,イスに乗っても,ひもの両端を同時につかむことはできません。さあ,どうしますか?
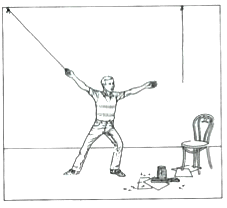
メイヤーの2本のひも問題では,下のYouTubeビデオに例が示されているように,部屋の中にあるプライヤー(ペンチ)をおもりの代わりとして使って,それを使ってひもを振り子のように揺らして解決する必要があります。しかしながら,一般的にプライヤーは何かを挟むための道具として認知されているので,参加者はおもりとしての用途を思いつきません。このように,私たちがものを認識するとき,それがもつ機能も同時に知覚されるのですが,それによって心的制約が生じて,そのもの本来の機能以外の使い途を思いつかないことを「機能的固着」(機能的固定)と呼びます。
2本のひも問題解決法です (YouTubeって何でもあるんですね ^^;)
問題解決の情報処理
さて,「思考」(考える)という行為は,ある種の問題解決と考えることができるので,このような思考問題を使ったたくさんの研究が古くからおこなわれてきたわけです。では,このような問題を,情報処理課題としてとらえた場合,どうすればそれを解決することができるようになるのでしょうか。
「ハノイの塔」という伝統的なパズルがありますが,それを題材に情報処理課題としての問題解決の方法の一例をご紹介します。ハノイの塔は下のようなパズルです(これは,教材用に3段に簡略化しています。ちなみに私が自作しました ^^)。

今回の課題は,上の写真で左側のピンにある3枚の円盤を,下の写真のように右側のピンに移動させるというものです。

ただし,ハノイの塔では,円盤を動かすのにはルールがあって,1回につき1枚ずつしか動かせません。また,下の写真のように,小さな円盤の上に大きな円盤を乗せることはできません。

みなさんも,紙の上に3つの円を描いて,500円玉,100円玉,1円玉を3つの円盤に見立ててやってみてください。一番左のピンから,一番右のピンまで,最短で7手で動かせるはずですが,できますか?
それでは,このパズルを情報処理の課題として解く方法を説明します。これを情報処理課題として記述することができれば,人間の代わりにコンピュータで解くことも簡単にできてしまうはずです。下の図では,一番大きな円盤を「LLL」,中くらいの円盤を「MM」,一番小さな円盤を「S」として,3つのピンの位置に描いたものです。スタートの状態である3つの円盤が一番左にある状態を一番上の「状態1」に置いています。その状態から,次の手としてどのような手があり得るかを赤い線でつないで「状態2」と「状態3」に描いています。「状態2」はSを一番右に移動した状態,「状態3」はSを真ん中に移動した状態ですね。また,「状態2」からは,「状態4」にするか「状態1」に戻るかしかありません。このように,すべての状態から,どのように変化させることができるかを すべて図にしてつないで配置したのが,この図ということになります。これを「基本問題空間」といいます。
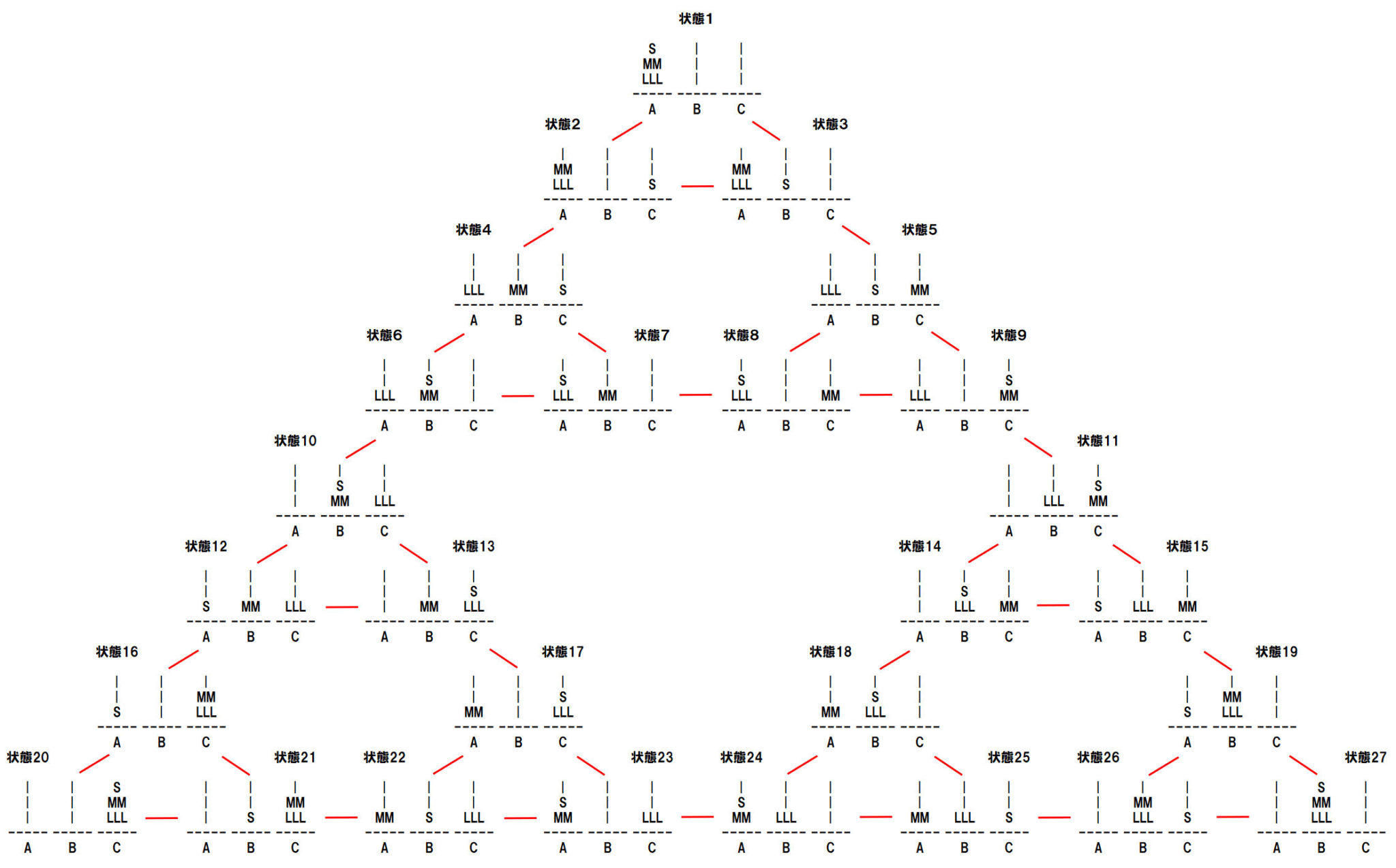
この基本問題空間において,スタート地点は一番上の「状態1」に描かれています。また,ゴールである3つの円盤を右のピンに移動した状態は,左下の「状態20」にあります。問題解決を情報処理課題としてとらえるときには,「問題のある状態」を,「現状と目標の間にギャップ(距離)のある状態」ととらえます。となると,「問題解決」とは,「現状と目標の間の距離を縮めていくこと」と考えられるわけです。したがって,この基本問題空間さえ記述できれば,あとは,その地図の中で目標に向かって道をたどって移動していけば,最終的に問題は解決できるというわけです。数えてみるとステップ数は7つになりますし,実際,そのように円盤を動かしていけば7手でこのパズルを解くことができます。
これが,思考の対象となる問題を,コンピュータのような計算機で解くときの考え方であり,基本的方法です。
手段-目的分析
ニューウェルたち(Newell, Shaw, & Simon, 1958)は,「一般問題解決プログラム」(General Problem Solver, GPS)という 問題解決を行うための情報処理システムを提案しました。そのプログラムでは,(1) まず,初期状態と目標(目的)の間にどのような差(ギャップ)があるかを認識します。(2) その差を埋めるために役立つオペレーターを選択します(「オペレーター」は,コンピュータでいうところの「演算子」で,「操作」あるいは「手段」と読み替えてください)。(3) その手段を講じるための下位目標を設定し,そのためにまた手段-目的分析を行います。人間が問題解決を行うときには,このように大きな目標を達成するために必要な手段を考えて,その手段を講じることを目標に設定したときに,また必要となる手段を考えて…というようにして,問題解決を行うので,それをシステムとして作れば,問題解決を行うプログラムができるというものです。
みなさんの中にも,「将来,何か人の役に立ちたい」という目的があって,そのために例えば「カウンセラー」という手段を選んで,じゃぁ「カウンセラーになる」という目的を設定したときに,その手段として考えられるのは「公認心理師」を取得するということで,そのためには「心理の大学」に…という感じで入学してきた人はいらっしゃるでしょう。これが,「手段-目的分析」という考え方です。
人間が行う問題解決の特徴
上のように考えれば,コンピュータでも問題解決ができるように思われますし,私たち人間もそうやって問題解決をしているように感じますが,必ずしも人間ってそんなに機械的に問題解決をやっているわけではないということも知られています。
まず,上のハノイの塔で紹介したような問題解決の方法を「アルゴリズム法」と呼びます。アルゴリズム法は,基本問題空間を描き出して,そのすべての状態をしらみつぶしに試していく方法であって,コンピュータ向きの解決方法です。例えば,下に例を示す迷路の実物大の模型があって,そこに私たちが実際に入って行ったとしましょう。上から見れば簡単な迷路も,中に入れば,どっちを向いているかさえすぐにわからなくなるので,とても難しい課題になります。

そういったときに,時間はかかるけれども,確実に迷路の出口にたどり着く方法として「右手法」や「左手法」という方法があるのをご存じでしょうか。要するに,右手あるいは左手をずっと壁につけて離さないように歩いていくのです。すると,時間はかかりますが,必ず出口にたどり着けます。下の図は,左手を壁につけたまま歩いていったときの軌跡になります。
-768x483-1.jpg)
上の例では,左手法にしたのですが,もし右手法を使ったならば,とんでもなく長い距離を歩くはめになったことは容易に想像できるでしょう。コンピュータで迷路課題の答えを探すときは,コンピュータは基本的に単純な計算処理は極めて高速なので,この右手法・左手法を使ってもあっという間に課題を解くことができます。しかし,人間の場合は,この方法で出口にたどりつくことがわかっていても,出口が見えるまで我慢できる人はなかなかいません。数学ドリルの計算問題のように,すでに手続き(アルゴリズム)を知っているルーチン的な(ワンパターンの)課題を除けば,人間が問題解決を行うときにアルゴリズム法を使うことはほとんどないのです。
人間が問題解決を行う場合によく使う方法は「ヒューリスティックス法」(発見法)と呼ばれます。この方法は,うまく行く保証はないけれども,以前の経験などに頼って,とりあえず役に立ちそうな方法をやってみるというやり方です。上の迷路なども,私たちが解くときには,「まずこっちに行ってみよう」というような感じで,試行錯誤を行うのが一般的な行動パターンでしょう。
日常の問題解決の多くについて,私たちは,この「ヒューリスティックス法」と,先に述べた「手段-目的分析」を合わせながらゴールを目指すのが一般的だと言われます。
人間だからつまずく問題
私たちが問題を解こうとすると,ほとんどの人が手詰まりになるので有名な思考問題に「宣教師と人食い人種」と呼ばれる問題がありますので,これも紹介しましょう。
【問題】
3人の宣教師と3人の人食い人種が旅をしていたところ,川にさしかかりました。川にはボートが1隻あるのですが,ボートには一度に2人しか乗ることができません。また,困ったことに,人食い人種たちは,自分たちの人数が宣教師よりも多いとわかると,宣教師を食べてしまおうとする悪い癖があります。宣教師の数が人食い人種の数より少なくならないようにして,全員が川向うに行くにはどうすればいいでしょうか?

なんで人食い人種のような面倒な人たちと旅をしてるんだよ (^^;)…なんていう突っ込みはとりあえずおいといて,紙の上に川を描いて,どっちでもかまわないけど,100円玉を宣教師,10円玉を人食い人種,消しゴムかなにかをボートというように見立てて,問題を解いてみてください。
(1) ボートには,2人しか乗れないので,最初の1手は次の2つしかありません。宣教師と人食い人種が1人ずつ乗って渡るか,人食い人種が2人乗って渡るか…ですね。宣教師が2人乗っていっちゃったら,残った宣教師は食べられてしまいます(これは…,見たくないわ…)。


(2) そのあと,次の人たちが川を渡るには,誰かがボートを返しに行かなければなりません。これは面倒ですねー。宣教師と人食い人種で渡った場合は,人食い人種がボートを返しに行くと,元の岸にいる2人の宣教師に対して,人食い人種の数が3人になっちゃいますから,この物語はホラーになってしまいます(あぁ,見たくない…)。というわけで,ボートを返した後は,下の図のパターンしかないはずです。

(3) 次に渡る2人は誰にしましょうか。宣教師2人が渡ると元の岸で血が流れます。宣教師と人食い人種で渡ると渡った先で血が流れます(あぁ,見たくない…)。というわけで,乗っていく2人は人食い人種たちということになりますね。

(4) 上の図は,人食い人種とお別れするチャンス!のように思いますが,行きたいのは川の向こうなので,ここはひとつ我慢しましょう。下の図のように,人食い人種がボートを戻してくるのを待ちます… ┐(´д`)┌。

(5) 次にボートに乗る2人は,宣教師2人しかないですね。食べられないとわかっていても,一人残される宣教師役にはなりたくないです… ( ̄▽ ̄;)。

(6) さて,自分でやってみた人の多くは,ここで「ツンダかも…」 と なりませんでしたか? 上の状態から,宣教師がボートを返しに行くと残った宣教師が食べられちゃうし,人食い人種が返しに行くと,心細い思いで一人残されていた宣教師がほんとにオワッテしまいます。
この問題を先に進めるために必要な,次の一手は,「宣教師と人食い人種が一緒になって2人でボートを返しに行く」ことなのです。でも,私たちは,「手段-目的分析」によって,目標(ゴール)に近づこうとしています。これが心的制約となって,せっかく対岸の人数が4人に増えたのに,また2人に戻してしまうという,目標からいったん「遠ざかる」方向の,下の図の考えがなかなか思い浮かばないのです。だから,途中で間違ったかな…と思って,また最初からやり直してしまう。そして,それを繰り返して,解けないのですね。

(7) 上の図の手ができたら,あとは簡単です。次は,宣教師が二人で対岸に渡ります。

(8) そのあとは,下の図のように人食い人種にボートを戻してもらいます。

今ですね… (★。★)/。ここでボートを爆破!すれば,あとは楽しい旅が待っています 。
…なんていう冗談はおいときまして,こんな感じで,あとはお好みに応じて人食い人種もこっちに渡ってきてもらって,ドキドキ・ワクワクのワンチーム旅行を続けることができるわけです。
いつか,彼氏 (彼女)と二人っきりでボートに乗ることがあったら,ぜひこの話を思い出してください (^^)。
推論
くだらない話をしていたら,8000文字書いたのに,まだ終わりません(泣)。
「思考」の心理学をお話しする上で,もうひとつ取り上げなければならない重要なトピックが「推論」です。
私たちは,知らないことについても,すでに経験した情報に基づいて,推し量ることができます。これが推論であり,私たちの日常を支えるもうひとつの大切な思考の働きです。
推論には,「演繹的推論」と「帰納的推論」の2種類があります。
演繹的推論
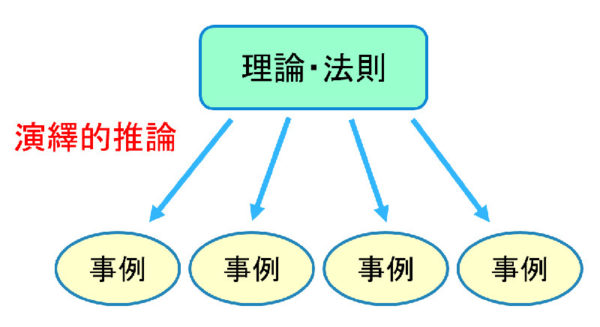
ウィキペディアによれば,演繹とは,「一般的・普遍的な前提から,より個別的・特殊的な結論を得る論理的推論の方法」と説明されていますが,要するに,演繹的推論とは,下の図のように「理論や法則をもとに,個々の事例について推論する」ことだと考えてください。俗に言われる「血液型性格」は科学的根拠がまったくないウソなので適切ではないかもしれませんが,(わかりやすいので)あえて例にすれば,「A型は几帳面だ」という法則があったとして,「吉田くんはA型だから,几帳面に違いない」と,個々のケース(事例)について推論するようなものです。
帰納的推論
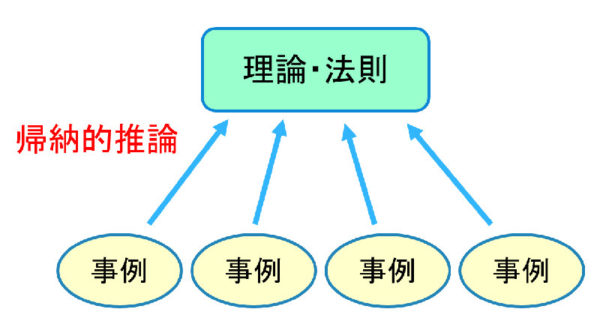
帰納とは「個別的・特殊的な事例から一般的・普遍的な規則・法則を見出そうとする論理的推論の方法」と説明されていますが,要するに,帰納的推論とは,「個々の事例をもとに,それらを包括する理論や法則を推論する」ことだと考えていただければと思います。血液型性格のたとえで言えば,「さとしくんはA型で几帳面」,「ひろしくんはO型でいいかげん」,「はなこさんはA型で几帳面」,「たけしくんはAB型でいいかげん」,「たろうくんはA型で几帳面」,「さとみさんはB型でいいかげん」…とたくさんのケース(事例)に出会う中で,「A型の人って几帳面じゃないの?」という法則を推論するようなものです。
演繹的推論の例:4枚カード問題(ウェイソン課題)
ウェイソンたち(Johnson-Laird & Waison, 1970)は,次のような演繹的推論の問題を使った研究を行いました。
【問題】
下の4枚のカードには,全て片面に数字が,もう一方の面にはローマ字が書いてあります。「もし,カードの片面にローマ字の母音が書いてあれば,その裏面の数字は偶数である」という規則が成立しているかどうかを調べるためには,最小限,どのカードをめくればよいでしょうか?

みなさんは,どのカードをめくればいいと思いますか?
実験の結果,イギリスの大学生の正解率は10%以下で,およそ50%の学生が「A」と「4」を選択し,35%が「A」のみを選択したと言われます。
母音の裏には偶数が書かれていなければならないので,「A」をめくるのは正しいのですが,もう1枚めくらなければならないのは「5」のカードであって,その裏が「母音でない」ことを確認する必要があるのです。
この結果について,ジョンソン・レアードたち(Johnson-Laird, Legrenzi, & Legrenzi, 1972)は,4枚カード問題を次のように作りなおしたところ,ほとんどの人が正解することを見出しました。日本の郵便局にも,「書籍」や「カタログ」を送るための「ゆうメール」サービスというのがあって,「信書」と呼ばれるプライベートな手紙よりも安い料金で送ることがありますが,これを利用するには,(信書が入っていないことを示すために)一部中身の見える透明な封筒を使うか,封筒の一部を開いた状態で送る必要があります。
【問題】
「もし手紙が密封されていれば,開封のままの手紙より10リラ多い50リラの切手を貼らなければならない。」 この規則が守られているかどうかを郵便局員がチェックするためには,どの手紙を調べればいいですか?
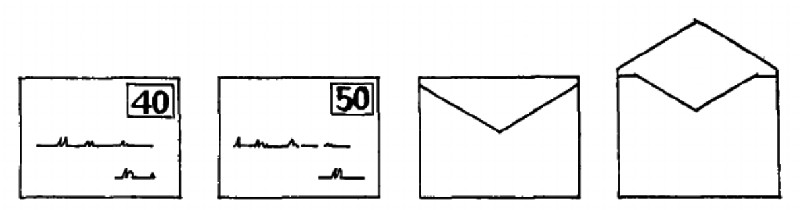
正しい答えは,右から2番目の封をしてある封筒が50リラの切手を貼ってあるかを確認するのと,40リラの切手が貼ってある封筒が開封された状態かということになりますね。
同様に,「20歳をすぎなければアルコールを飲んではいけない」というルールが守られているかどうかを確かめるには,以下の4人のうちの誰を調べなければならないか…という問題については,どうでしょうか。
- ビールを飲んでいる人
- コーラを飲んでいる人
- 何か飲んでいる25歳
- 何か飲んでいる16歳
おわかりだと思いますが,同じ論理構造の問題なのに,損得の問題やルール順守の問題に置き換えると,私たちは直感的に短時間のうちに正しい判断を行うことができることがわかります。このようなことから,このウェイソン課題は,知能の進化や 社会的裏切りに対する感情判断などの観点から,進化心理学や行動経済学における研究がなされていて注目されています(リンク:ウェイソン選択課題)。
帰納的推論の例:ブルーナーらによる概念形成の研究
演繹的推論は,規則や前提から結論を必然的・論理的に導くものなので,正しく行われている限り 間違うことがないのに対して,帰納的推論は,多くの事例を経験する中で,必然ではないけれどももっともらしい結論を導き出すものなので,常に間違いを伴うリスクがあります。何か新しい食べ物をみて「これはおいしそうだ」と推測するのも帰納的推論なのですが,外れた経験は誰でもあるでしょう。でも,演繹的推論が本質的には知識を増やさないのに対して,帰納的推論は,たくさんの事例を一般化することで概念を形成したり,それをもとに類推したり,因果関係を推論するなど,私たちが日常生活の中で,知識や概念を形成していくために重要な役割をもっていると言えます。
帰納的推論によって導かれる結論は,常に暫定的なもの(仮説)でしかありませんので,それを吟味する仮説検証の過程が重要な役割をもっています。ブルーナーら(Bruner, Goodnow, & Austin, 1956)は,どのように仮説が作られ,経験によって修正されていくかを調べる方法を開発しました。
彼らは,下に示すような,図形の色,図形の形,枠の本数,図形の個数(それぞれ3種類)を組み合わせた81個の図形について,実験者があらかじめ正解とする概念(たとえば,○が2つなど)を決めておいて,次々に参加者に提示します。参加者は,実験者がもっている正解の概念を知らないまま,提示されるパターンが実験者が考えている正事例か,それとも負事例かをあてていき,その判断ごとにそれが正解か誤りかをフィードバックされます。できるだけ少ない回数で,実験者が想定している人工概念をあてるため,参加者は,概念についての仮説を立て,新しい事例ごとに仮説を検証し,必要に応じて仮説を修正していきます。
このような実験を行うことで,人がどのように概念を形成していくかを調べた結果,参加者が取る方略には「全体方略」と「部分方略」があることがわかりました。全体方略では,最初の正事例がもつすべての特徴が概念であるという仮説が立てられて,この仮説に合わない事例に出会うと,不適切な特徴が削られていきます。それに対して,部分方略では,最初の正事例から,例えば「2つ」など,可能性の高そうな特徴だけを選び出し,負事例に出会うと,仮説をまた立て直すという方法を取りますが,この方略では,過去の事例についての正確な記憶がないと,過去の事例に矛盾しない新しい仮説を立てることができず,記憶容量に限界のある私たちにとっては,一般には失敗しやすい方略となります。彼らの実験では,知的水準の高い回答者ほど全体方略をとることが明らかになりました。
帰納的推論の例:ベイズ確率問題
帰納法では,不完全なデータに基づいて仮説を得ようとするので,常に不確実性のもとで結論を導かなければなりません。「ベイズの定理」は,あるデータが与えられた場合に,ある仮説が真である確率を求めるもの(だそう)です。
ベイズ推定の例としては,いくつかの袋があって,その中に赤い玉と白い玉がいくつか入っているとします。これらの袋のうちどれかひとつの袋から,いくつかの玉を取り出します。この取り出された玉の色を データ(結果)として,それがどの袋から取り出されたものか(原因)を推定するようなときに使える方法です(リンク:ベイズの定理)。
難しい話はとりあえずおいといて,思考の心理学で扱われるベイズ確率の問題は以下のようなものです(この例のように,病気の確率を使った問題もあれば,交通事故を起こしたタクシー会社を問題にする「タクシー問題」なども有名です)。
【問題の例】
あるガンにかかる確率は0.01%(0.0001;1万人に1人)です(事前確率)。ある検査を使うと,95%の確率の確率でそのガンにかかっているかどうかがわかります(条件つき確率)。職場の健康診断で,あなたが検査を受けてみたところ,陽性という結果が出ました(ガーン! ><;)。あなたがこのガンにかかっている確率は?(事後確率)
このような問題を出すと,直感による人々の確率評価は事前確率を無視する傾向にあり,ベイズの定理から与えられる合理的な数値と大きくずれてしまうことが知られています。みなさんも,検査が95%の確率でガンかどうかを診断できるのだから,自分がガンにかかっている確率は95%だと思いませんか?
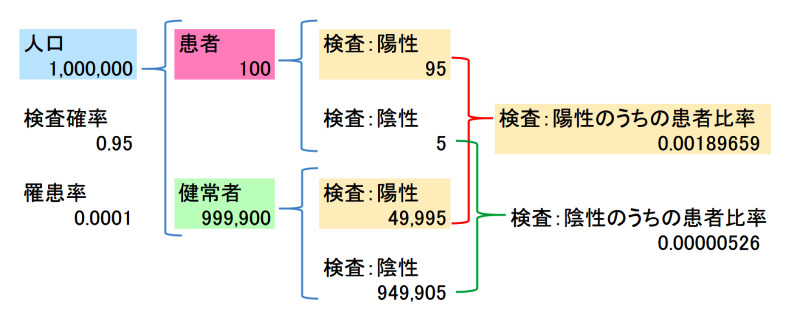
ベイズ確率を説明するために,下の図のようなシミュレーションをおこなってみましょう。住民が100万人の市を想定します。すると,ガン患者は1万人にひとり(0.01%)なので,100人いることになります。それに対して,ガンでない人は99万9900人になります。全員に検査を受けさせると,検査の確率は95%なので,100人の患者のうちの95人は検査結果が陽性になります。その一方で,5人は陰性(偽陰性)となります。また,健康な人も検査を受けると,その95%である94万9905人は検査結果は陰性ですが,5%に相当する4万9995人は偽陽性の反応が得られます。となると,検査結果が陽性と出るのは49,995+95人で5万90人となり,そのうち本当のガン患者は95人ですから,検査結果が陽性の人のうち,本当の患者比率はおよそ0.2%(0.0019)となるのです。
現在流行している新型コロナ感染症に対するPCR検査のように,きわめて高い確率で感染していると疑われる人だけを対象にした検査では,検査結果の意味も変わってくるでしょうが,全員が受ける検査で陽性反応が出る確率はこのような仕組みになるのです。
でも,私たちは事前確率を無視する傾向があるため,それを錯覚してしまうのですね。
出席確認
引用文献
- Bruner, J. S., Goodnow, J. J., & Austin, G. A. (1956). A Study of Thinking. New York: Wiley.
- Johnson-Laird, P. N., Legrenzi, P., Legrenzi, M. S. (1972). Reasoning and a sense of reality. British Journal of Psychology, 63, 395–400.
- Johnson-Laird, P. N. & Wason, P. C. (1970). A theoretical analysis of insight into a reasoning task. Cognitive Psychology, 1, 134-148.
- Newell, A., Shaw, J. C. & Simon, H. A. (1958). Elements of a theory of human problem solving. Psychological Review, 65, 151-166.
