5: 実験法(2)

maruhi コメントを受け付けていません

（公開日：2020年5月14日）

この心理学研究法の話も，だんだん難しくなってきたと思っている人が多いと思いますが，今日もちょっぴり難しい話をさせていただきますね。

今，「実験法」の話をしていますが，観察法，実験法，調査法，検査法，面接法のうち，実験法，調査法，および検査法の一部では，人間の心理・行動の特性を，何らかのかたちで数値として測りとろうとします。私たちそれぞれが個性としてもっている性格や知能なども，数字でとらえようとするわけですね。

すると，心理学では，どうしても統計法という数学についての知識が必要になります。今日の授業の最初では，この統計法の考え方について話をさせてもらいます。ちょっと難しいと感じる人が多いと思いますが，今日の授業ですべてを理解できる必要はありません。統計法については，後期に「心理学統計法」という授業（伊藤先生担当）があって，そちらで詳しく習いますから大丈夫です。ただ，人間の心や行動という誤差の多いものを科学的に扱うとき，統計法の考え方は欠かせません。この統計法の考え方のベースには「確率」があります。今日は，この確率の話から始めます。

超能力実験

最初にちょっとした実験をやってみましょう。全然，心理学とは関係ない実験なんだけど，この授業は心理学の授業だから，「超心理学」（超能力）に関する実験ということにしましょう。皆さんは自分に超能力があると思いますか？

では，みなさんの超能力をこれから実験で測ってみます。コインを１枚，出してください。そのコインに向かって，「オモテになってね」とやさしく願いをかけてから，指ではじいて投げ上げてください。

…オモテが出ましたか？

では，この実験を５回続けましょう。きちんと記録を取ってくださいね。

下の表が私の記録です。

試行	結果
１回目	ウラ
２回目	オモテ
３回目	オモテ
４回目	ウラ
５回目	ウラ

５回中３回もウラが出てしまいました。どうも私には超能力はないみたいですね。皆さんはどうでしたか？５回連続オモテが出た人はいらっしゃいますか？（いたら私にテレパシーで伝えてくださいね…メールは不要です）

確率を使って物事を考える

先ほどの実験は，単純に確率で考えることができます。コインのオモテが出る確率は0.5ですから，５回連続でオモテが出る確率は，0.5×0.5×0.5×0.5×0.5と，0.5を５回かけることで計算できます。その答えは0.03125ですね。約3%なので，もしあなたが５回連続オモテが出たとすると，100人中３人しかできなかったようなすごいことを成し遂げたと言えるわけです。

この実験では，コインのウラを出さないことが大事なのですが，下の表は，ウラが出た数と，その数だけウラが出た人の割合として期待される確率，およびウラがその数以下だった人がどれだけいるかの割合（累積確率）を示したものです。この表で見ると，ウラの数が０回という人は３％くらいなので少ないといえるのですが，ウラの数が１回以下の人となると累積確率は18.75%に跳ね上がりますから，５人に１人くらいはそういう人もいるよね…と考えられるわけです。ウラが２回以下の人で考えると累積確率は５割（0.5）ですから，珍しくもなんともないわけです。

ウラの数	確率	累積確率
0	0.03125	0.03125
1	0.15625	0.18750
2	0.31250	0.50000
3	0.31250	0.81250
4	0.15625	0.96875
5	0.03125	1.00000

下の図は，上の表をグラフにしたものです。「有意水準」というのですが，心理学など社会科学の領域では累積確率が５％（0.05）以下のところに「意味がある」と考えるレベルを設定するのが一般的です。これを「有意確率５％」（あるいは「有意水準５％」）と言います。５％は20分の１なので，20回やって１回しか得られないような結果が，１回だけの実験で得られたとなると，その結果は単なる偶然とは考えられないのではないか，よって「意味がある」と考えましょうというわけです。ですから，今回の実験では，ウラの数が０回の人は「有意に超能力があるとみなされる」わけですね。おめでとうございます！

片側確率と両側確率

みなさんの中に，「ちょっと待ってよ！私，１回もオモテ出なかったんだけど…。私にも超能力あるんじゃないの？」という人いらっしゃいませんか？（私も，昔10人連続でじゃんけんに負けたとき，「自分は何かもってる！」と思いました ^^;）

人間の心や行動を含むいろいろな現象を測定すると，そのデータには個人差や偶然の誤差などさまざまな要因によるばらつきが含まれます。下の図は，平均を０，標準偏差を１とする「正規分布」なのですが，ばらつきをもつデータは基本的にこのような釣り鐘型の分布をもっています。累積確率はこのようなグラフ上では面積で表せるのですが，先ほどの実験は「オモテになってね」と願いをかけたので，ウラが出た数が少ない人しか問題にしていませんでした。実験において，あらかじめ「こっちの方が多いはずだ」というような明確な仮説があるときには，このような感じで，ばらつきの一方の側しか問題にしません。例えば，新型コロナ感染症の治療薬の効果を見る実験であれば，薬を投与することによって症状は「改善されるはず」ですから，逆方向を考えることはありません。このような考えで有意確率を扱うときには「片側確率」という言葉が使われます。

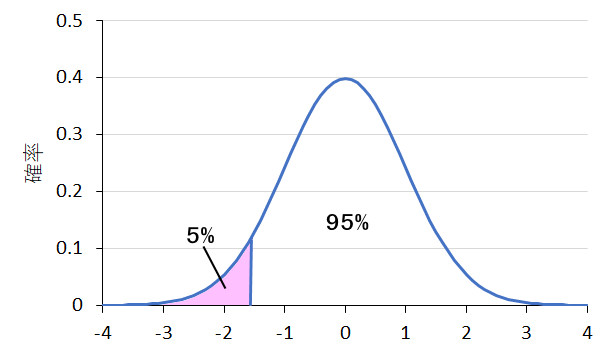
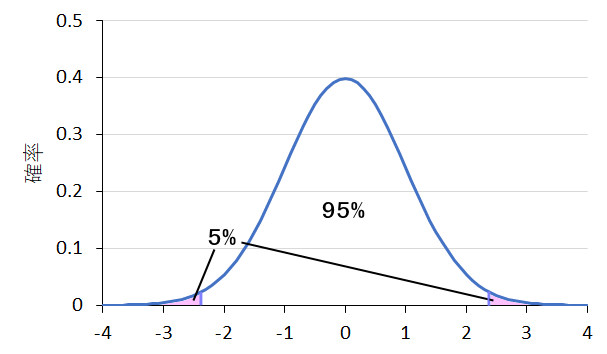
でも，科学における多くの研究では，そういった一方向的な仮説をもたずに結果をとらえようとすることも少なくありません。そういったときには，下の図のように両端を合わせて5%という確率を考えます。この考え方で有意確率を問題にするときには「両側確率」という言葉が使われます。とにかく，多かったり少なかったり，どちらでもいいけど，合わせて５％の確率でしか起こらないことが１回の実験で結果として得られたら，何か意味のある現象がとらえられたんだ！…と考えるわけです。このあたり，みなさん１年生だから，まだ理解できなくていいけど，「ふ～ん，そんな言葉があるんか～」くらいには記憶にとどめておいてくれたらうれしいです。

イヌ・ネコ対決！

「知覚・認知心理学」の授業の履修確認時に，みなさんは「イヌ派？」，それとも「ネコ派？」という調査をしました。覚えておいでですか？

その結果を下に示します。回答数91人中，イヌ好きが50人（55%），ネコ好きが41人（45%）でした。

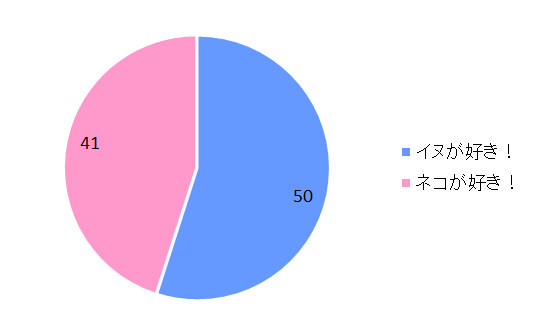
この調査結果だけから見ると「イヌ好き」が多いようです。でも，今回は91人の大学１年生を研究対象（サンプル）として抽出して調査したけど，同じような調査をまた別の91人に対して行えば，違う結果が得られるかもしれませんよね。つまり，このイヌ好きが多いという結果は，単に今回の91人に限定された，単なる「誤差」を反映している可能性もあるのです。

そこで，科学では，次のように考えます。

まず，「イヌ好きとネコ好きは同数」であるという仮説を立てます。このような仮説を「帰無仮説」と言います。仮説のことを英語でhypothesisというので，その頭文字にゼロをくっつけてH0なんて書いてある専門書が多いかな。この帰無仮説とは，言葉通り「無に帰す」ための仮説で，これをポイっと捨て去る（「棄却する」）ことで，こっちが多いということを証明するのです。なんでこんな面倒なことをするのでしょうか？実は，とりあえず，イヌ派とネコ派が同じはずだと仮説を立てたら，そんな集団から91人を無作為（でたらめ）に選んできて「あなたどっち派？」って尋ねたら，こんな結果になるはずだという予測をすることが数学的に可能だからです。要するに，オモテとウラが半分半分に出るコインを，91回投げてみるんですね。その時何回オモテ（あるいはウラ）が出るかの確率を求めるのです。その確率は，グラフにすると次のようになります。

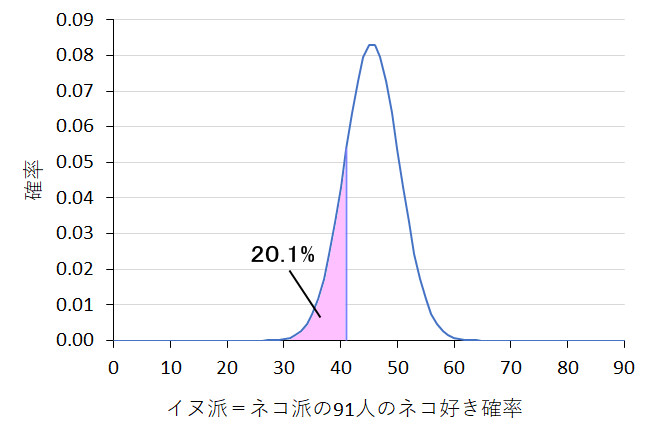
イヌ派＝ネコ派なので，91人中，ネコ派は45人か46人になる確率が一番多いのですが，41人という確率も結構あって，41人以下になる累積確率を計算すると20.1%もあるのです。これは片側確率なので，誤差によってネコ派が多くなる逆側も考えるなら，このように中央から４～５人以上偏った結果が得られる確率は，２倍の40.2%あるということになります。となると，今回の調査結果をもって「イヌ派がネコ派よりも多い」という結論を下すのは難しい（つまり，帰無仮説を棄却できない）ということになります。ちなみに，91人の調査だったら，ネコ派が37人以下なら片側確率5%で，35人以下なら両側確率5%で「イヌ派が多い」と結論づけられることになります。

統計検定

ちょっと難しかったかもしれませんが，このように確率を使って，得られた結果を，誤差と考えた方がいいのか，それとも20回中１回しか見られないことが１回の実験で得られたので意味があると考えて構わないのかという判断基準を与えてくれるのが「統計検定」です。上の例は「二項分布」という二つの現象が起きるときの確率分布を使って説明しましたが，測定を通して得られた値の差の有意性についても同様に検定を行うことができます。

たとえば，「ｔ検定」という統計検定は，得られた２つの平均値の間に統計的に（確率上）意味のある差（「有意差」）があるかどうかを検定する有名な方法です。また，「分散分析」という方法も，２要因以上の実験計画や，１要因でも３水準以上の結果の分析に使える統計検定として有名です。

下のグラフは，統計データを基に作った大学生の身長の分布です。みなさんは，この分布のどこにいらっしゃいますか？身長には個人差があるので，分布には必ずばらつき（幅）があります。このばらつきのことを「分散」といいます。

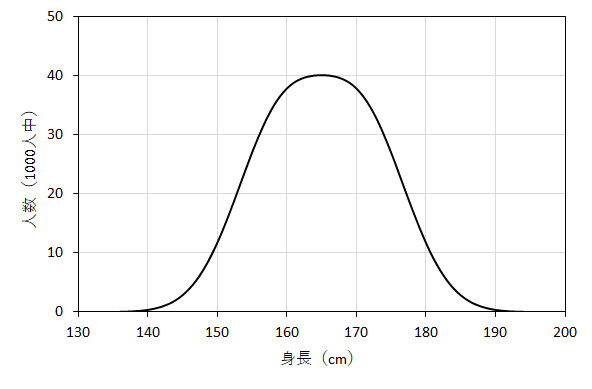
大学生によってつくられている上のグラフは，実は２つのグループから構成されています。男性と女性です。では，全体のデータを，男性と女性という２つのグループに分けるとどのようになるでしょうか。下の図のように，全体のデータがもっていたばらつき（分散）は，男性・女性それぞれのグループがもつ個人差（これを「誤差」と呼びます）と，男性・女性がもつ「差」（性の「効果」と呼ぶこともあります）に分けられます。仮に，男性と女性の間に本来身長の差がないとすれば（帰無仮説），このようなばらつきをもったデータならばこれだけの人数のサンプルをとったとき，その平均値にはこの程度の偶然の差は出るはずだという予測を立てることができます。その予測よりも大きな差が得られたとすれば，男女の身長は何％水準で有意に男性の方が高いと結論できるわけですね。これがｔ検定や分散分析の（とても大まかな）仕組みです。

要因計画に基づく実験計画

難しい話ばかりでごめんなさい。でも，あとのいろいろな授業で，必ず出てくる基本的な用語を，これでもできるだけ簡単に工夫しながら説明したつもりです。今回わからなくても，あとの授業で用語がでてきたときに，心理学研究法で習ったやつや～と思い出してくれたら，ありがたいです。私は認知心理学者ですが，記憶というものは覚えるだけでは定着しないもので，使うことで定着するのです（だから，テスト前に丸暗記したことはすべてなくなってしまうのです）。「あっ！これ知ってる！聞いたことある！」と思うとき，記憶は定着の作業を行っているのですよ。

それでは，前回の授業で取り上げた例を思い出してください。

学校の授業で行われる教育方法によって，どのように教育効果が違うのかを調べたいとします。どんな実験計画が考えられるでしょうか。まず，独立変数として操作すべき変数として，「教育方法」は絶対に必要ですね。また，従属変数として「教育効果」を測定しなければなりません。

まず，従属変数の方が簡単なので，先に従属変数を決めますね。

教育効果を測るのに，成績ややる気などいろいろあるよという話をしましたが，今回は，実験計画や結果の見方のサンプルとして取り上げるだけなので，従属変数としては「テスト成績」を指標とすることにします。

次は，実験計画（要因計画）の肝となる独立変数です。

教育方法については，講義型授業と体験型授業の２水準を設けることにしましょう。従属変数として測定するテスト成績は個人差が大きいので，この教育方法の要因は参加者内要因で実験することにします。つまり，それぞれの子どもが講義型授業も体験型授業も受けるわけです。順序効果が考えられるので，２つのクラスを研究対象にすることにして，一方のクラスは先に講義型授業を，もう一方のクラスは先に体験型授業を受けるというようにカウンタバランスをとることにします。

また，教育方法の１要因を問題にするだけでなく，あと２つ要因を加えましょう。ひとつは，生徒の性別（２水準：男子・女子）にします。男女で何か教育効果に違いがみられるかもしれませんから。また，もうひとつは，生徒の学力（２水準：高・低）にします。体験型授業は，学力が伸び悩んでいる子どもの教育にも効果が高いと言われますから，現在の学力と教育方法の交互作用が見られるかもしれません。この生徒の性別と学力は，どちらも参加者間要因になりますね。

では，実験で扱う独立変数を見てみます。要因計画を立てるときに，要因名にアルファベットを使うことがあるので，それに習って箇条書きにします。また，要因を並べるときに参加者間要因を先に書く習慣があるので，順番もそれに習います。

要因Ａ：生徒の性別（参加者間変数，２水準）
- 男子
- 女子
要因Ｂ：生徒の学力（参加者間要因，２水準）
- 学力高群
- 学力低群
要因Ｃ：教育方法（参加者内変数：２水準）
- 講義型授業
- 体験型授業

このような要因計画を，２×２×２の「３要因実験計画」と言います。この条件の組み合わせで，それぞれ授業後に「テスト」を実施して，教育効果を測定します。となると，２×２×２つまり８個の条件の組み合わせについて，テスト成績のデータを集計することになります。

実際にデータを見てみましょう。下に示したデータは，ずいぶん昔，比治山大学の「情報科学」という授業を講義室でやった場合と，コンピュータルームで実際にパソコンを使いながらやったときの成績データを，他の授業の成績を使って学力高群・学力低群に分類して集計したものです。これをダミーデータとして使います。

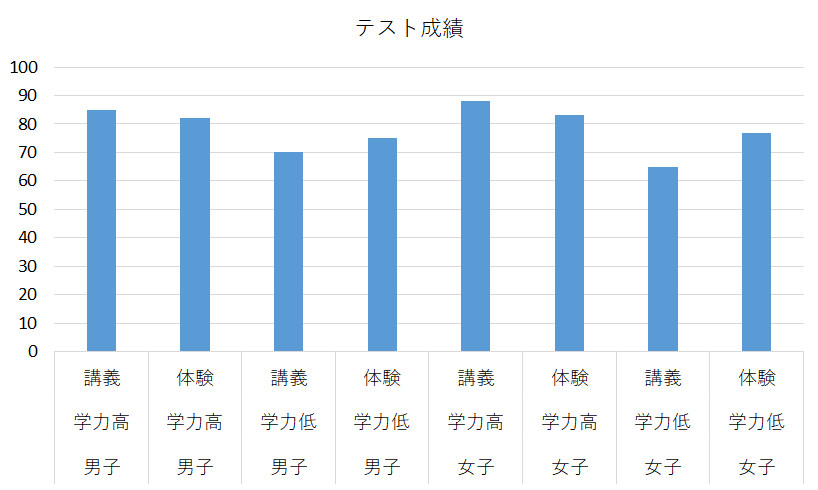
２×２×２で８つの条件の組み合わせがあるので，テスト成績の棒グラフが８本になっています。…が，これを見て，どのような結果になったかわかるでしょうか。すぐにはわからないかと思います。そこで，実際の実験では，このような要因計画で得られたデータを，先に紹介した分散分析という統計検定にかけます。分散分析は，前に書いたように，データに含まれるばらつき（分散）を分解（分析）して，男子と女子の違いが誤差に対してどの程度の差なのか，学力高群と低群の差は誤差に対してどの程度なのか，教育方法によってはどうか，また，交互作用についてはどうなのかといったところを調べてくれる方法です（実際には要因計画のパターンに基づいてデータをコンピュータに投入して計算を任せます）。

では，要因の組み合わせに従って，上のグラフを違った形で集計しながら見てみましょう。

主効果について検討する

今回は性別，学力，教育方法の３要因を扱った実験計画を用いています。「主効果」とは，それぞれの要因が単独に測定値（従属変数）にどのような影響を及ぼしたかという点を調べるものです。

下は性別の主効果をグラフにしたものです。上の図で示した８本の棒グラフを男女でそれぞれ集計して平均したものだと思ってください。分散分析の結果は，性別の主効果は有意ではない（つまり有意差はない）ということを示しました。実際に見ても，男女で得点に違いは見られませんよね。

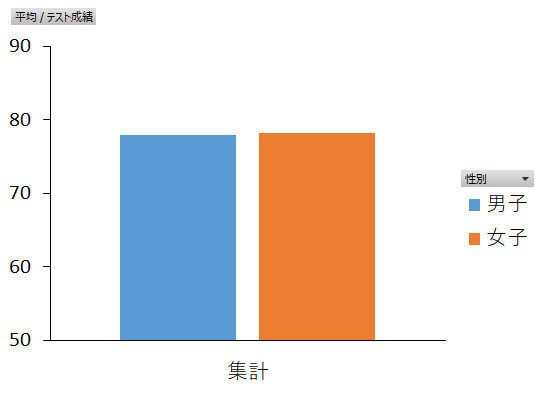
次の図は，学力の主効果をグラフにしたものです。分散分析の結果，有意水準５％で学力の主効果が認められ，学力高群の成績が低群の成績よりも良かったということがわかりました。つまり，この棒グラフに見られる得点の差は誤差とは考えない方がいいということになります。でも，よく考えれば，「テスト成績」を指標にしているわけなので，学力による違いがあるのは当たり前と言えば当たり前と言えます (^^;)。

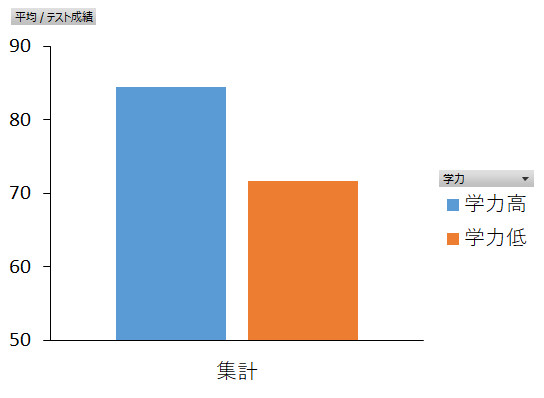
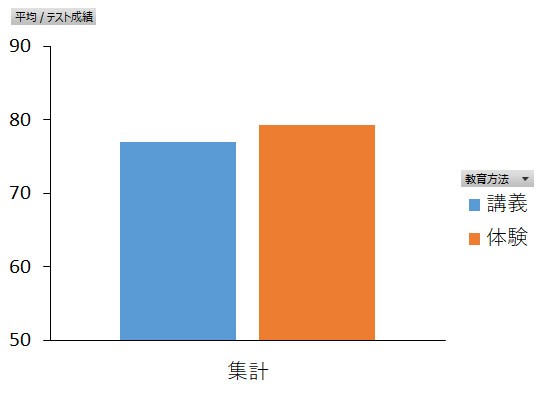
次は教育方法の主効果です。分散分析の結果，この主効果は有意とは認められませんでした。棒グラフを見ると，体験型授業を受けた人たちの成績が講義授業よりも少しいいように見えますが，これは誤差と考えた方がよろしいでしょうということになるわけです。

交互作用について検討する

実験法においては，要因計画を使ってきちんとした実験計画を組んで実験を行えば，交互作用についても検討することができます。この交互作用によって新しい発見がもたらされることも多いので，今回のデータについても見てみましょう。

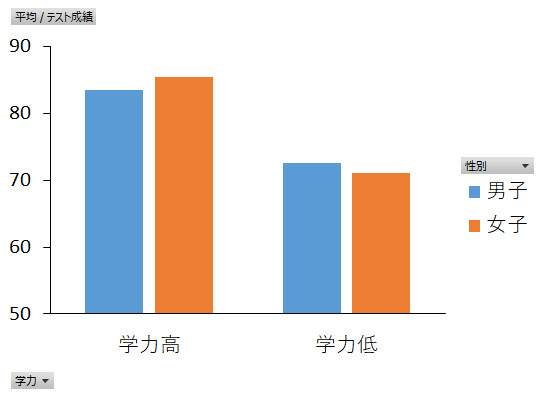
下の図は，性別×学力の２要因を組み合わせたグラフになります。分散分析の結果，この性別×学力の交互作用は有意ではありませんでした。先に学力の主効果が見られましたが，このグラフでもそこで見られた学力による違い以上の情報は特に認められないということになります。

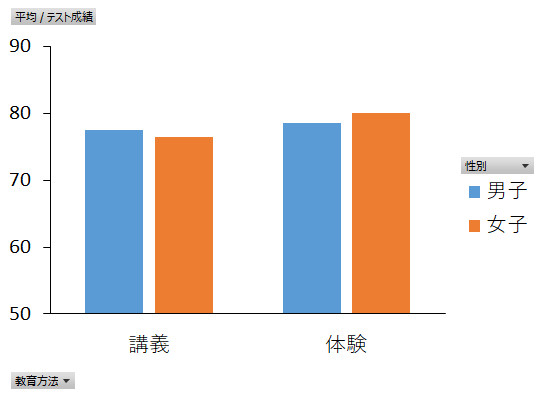
次は，性別×教育方法の交互作用を見るための図です。分散分析の結果，この交互作用も有意とは認められませんでした。主効果のところで，性別の主効果も教育方法の主効果も見られなかったのですが，ここでも特に特徴的な（誤差とは認められないような）結果は得られていないということになります。

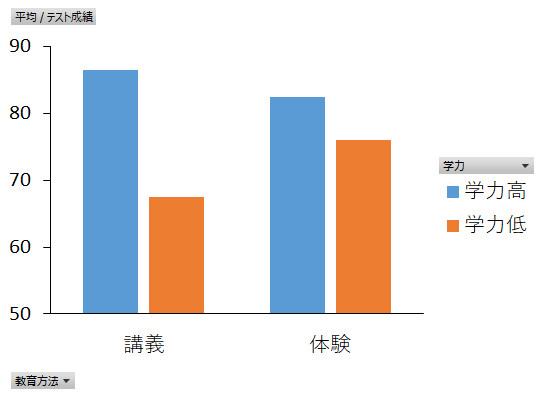
次にあげる学力×教育方法の交互作用については，分散分析の結果，５％水準で有意だったことがわかりました。こういう結果が新しい発見をもたらします。主効果のところで，学力高群の方が低群よりも成績がいいというのは当たり前の結果だねといいましたが，その学力による差は，講義授業では大きいのですが，体験型授業では小さくなっているのです。言い換えれば，学力高群は講義型授業でも体験型授業でも高い成績を示すのですが，学力低群は体験型授業を受けると講義型授業よりも10点近く高い成績を出しているわけなのですね。このことから，体験型授業は勉強でちょっと伸び悩んでいるような生徒に効果的な教育方法だということが結論づけられるのです。

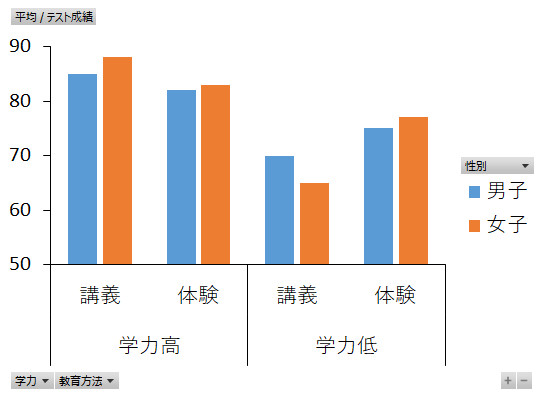
交互作用は，２つの要因の組み合わせだけでなく，３つ以上の要因の組み合わせでも生じることがあります。下のグラフは性別×学力×教育方法の交互作用の図ですが，分散分析の結果，この交互作用は有意ではありませんでした。３要因の交互作用は「交互作用の交互作用」なので「２次の交互作用」と呼びますが，これが有意になると，それを的確に説明するのに頭をひねって悩むこともしばしばです。

以上，今日の授業は統計の話が難しかったかなと思いますが，数値的データを使った確率統計の考え方と，要因計画を使った実験データの結果の分析はこんな感じでやるんですよという例をお示ししました。

お疲れさまでした。

~~出席確認~~　←　受講生は必ず回答してください！

（今回から，授業に対する意見・感想・質問を記入してもらう形式にします。「特になし」などではなく，必ず自分の意見・感想・質問を書いてください。それを評価対象とします）