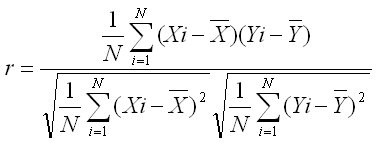心理学研究法Ａ

（公開日：2020年4月20日）

前回よりは難しいと思いますが，がんばって読んで，確認テストに解答してください。

日常における自然観察の限界

「オリエンテーション」の観察法のところで触れましたが，「観察」とは最も基本的な心理学の研究方法です。私たちも日常で人の行動を観察することで，相手がどんな人かを推測していますよね。自然な状態での（日常的な）対象の観察は「自然観察」と呼ばれますが，誰でも思いつくようなこの方法は，ときに誤った推論に人を導くことがあります。

というのは，日常での自然観察は，どうしても非系統的（物事の繋がりや順序を整理していない）であったり，偶発的（ちょうど偶然生じたことの観察）であったり，目立つ要因に注意が向きやすかったりするからです。また，きちんとした「記録」を取らず，「記憶」に頼ることも多いでしょう。そのために，自然観察では，ときに誤った因果関係の推論が行われやすいという欠点があります（「因果関係」とは原因→結果の関係を表す重要な用語なので後で詳しく説明します）。

その例をひとつ紹介しましょう。心理学を学んだことのある人ならほぼ誰もが聞いたことのある話です。1900年ころのベルリン（ドイツ）で，「賢い馬ハンス」と呼ばれた馬がいました。ハンスには特技があって，なんと，四則演算，分数・小数の変換，時計を見て時刻を答える，正しいスペルで単語を綴る…などができたのです。もちろん，ハンスは馬なのでしゃべることができません。そこで，ハンスは，飼い主のオステンさんの質問に対して，答えの数だけひづめで地面を叩いたり，正しいカードを鼻先で指し示して答えたそうです。下の写真は，Wikipediaに紹介されている，実際にハンスが計算をしているところの写真だそうです。

賢馬ハンス – Wikipedia

ハンスは本当に人間と同じような知能をもっていたのでしょうか？ 心理学者のプフングスト（Pfunngst, O.）が，それを科学的に検証する実験を行いました。彼は，ハンスに問題を出すとき，質問者が質問の答えを知っている条件（知識あり条件）と，知らない条件（知識なし条件）に分けて，ハンスの正答率を比較したのです。その結果，知識あり条件ではハンスの正答率は90%以上であったのに，知識なし条件では，正答率は10%程度に過ぎないことがわかりました。

このことから，ハンスは計算などができていたのではないと考えられます。ハンスがひづめを叩き始めると，質問者はハンスの足元に視線を落としますが，ハンスが正しい数を叩いた瞬間に，（それがちょうど正答にあたるので）質問者の体がどうしてもかすかに動いてしまいます（誰でも「おっ」とか「キターー！」って思いますよね）。ハンスはこの動きに反応してひづめの動きを止めていたのだと考えられています。後の研究では，馬は人間の顔の筋肉の1/60 mm の動きを弁別できることがわかっているそうです（大山正・中島義明，1993「実験心理学への招待」）。

モーガン（Morgan, C. L.）という生物学者は，「比較心理学入門」という本の中で，「モーガンの公準」と呼ばれる研究のガイドラインを提唱しています。これは，「ある活動が心理的により低い段階の能力を発揮した結果として解釈できるならば，その活動をより高次の心理能力の結果と解釈してはならない」というものです。動物などを被験体（実験対象）とした研究では，科学者としてもつべきとても重要な態度です。似たようなガイドラインは，実は学問の世界にはたくさんあります。例えば，「オッカムの剃刀（かみそり）」と呼ばれるガイドラインもとても有名です。これは，「ある事柄を説明するのに必要以上の仮説を立ててはならない」，また，「ある現象を同じ程度うまく説明する仮説が複数あるなら，よりシンプルな方を選ぶべきである」というようなガイドラインです。

実証（検証）することの重要性

皆さんは「血液型性格診断」って聞いたことありますか？ Ａ型は優しくて几帳面，Ｂ型はマイペースで新し物好き，Ｏ型はおおらかで行動的，ＡＢ型はドライでツンデレといったように（特徴はさまざまですが）血液型によって私たちの性格が異なるという考え方です。ちなみにこの血液型性格診断には，全く科学的な根拠がありません。血液型性格を提唱して世の中に広めた人に「能見正比古」という人物が知られていますが，Wikipediaの記事にはこう書いてあります。

• 能見 正比古（のみ まさひこ，1925年7月18日 – 1981年10月30日）は，日本の文筆家。人の血液型と気質とを統計的に関係付けたと称し，「血液型人間学」や「血液型性格分類」という占いを考案した人物。

血液型性格というものを信じる人はなぜか日本に多いのですが，これは「占い」なのですね。血液型というのは生まれたときから決まっていて，本人の努力などで変えられるものではありません。何の根拠もないのに，生まれもった性質によって「あなたは変わり者だ」などと言われるのは，世の中では「偏見」や「差別」と呼ばれる行為です。やってはいけないことですね。だから，わたくしたちは（心理学という科学を学ぶ人間ですから）このような間違った知識を世の中に広めてはいけません。

さて，では，この血液型性格という考え方が科学的でない（正しくない）ことは，どうすれば実証（検証）することができるでしょうか？

因果関係をとらえる

血液型性格は，「血液型が○○型の人は，性格が□□…」というように，「ＸならばＹである」という関係をもっています。このような関係性を表す言葉を論理学では「命題」といいます（さあ，難しくなってきた… ^^）。命題とは，それが「正しい」（真：「しん」と読む）か，それとも「誤り」（偽：「ぎ」）かという真偽判断の対象となるものです。じゃあ，血液型性格が本当かどうかを調べるには，それが「誤り」であること，つまり「ＸなのにＹじゃない」関係の存在を示せばいいですね。そこで，いろんな血液型の人を連れてきて，「性格検査」（検査法のところで習います）をやってもらって，Ａ型なのにＡ型の性格特徴が高い得点で出ていなくて，他の血液型に比べて変わらないなんてことを調べることで，この血液型性格が科学的に正しくないことを証明することができます。

科学というものは，世の中に起こっているいろいろな物事（現象）の中に，新たな命題を発見して紹介したり，まことしやかに言われている命題が正しいものかどうかを検証するのがお仕事です。「命題」なんて難しい言葉をあまり口にすることはないけど，いろいろな社会現象や人間行動の中に「命題」を見抜く目をもつことが，心理学を学ぶ上ではとても重要です。（赤字を追加しました。）

因果関係と相関関係

血液型性格が言うような「ＸならばＹである」という関係は「因果関係」と呼ばれます。原因と結果の関係ですね。因果関係では，「Ｏ型の人はおおらか」（←ウソですが）というような方向性をもっているので，「うちの子をおおらかな性格に育てたらＯ型になっちゃった」なんて逆方向の関係は含んでいません。あくまでも「ＸならばＹ」という「Ｘ→Ｙ」の向きだけの関係です。でも，世の中にあるさまざまな現象の中で「ＸならばＹ」の命題を探していくと，因果関係のように見えて，実は必ずしも「原因→結果」の関係とは言えないものも多いのです。

そこで，因果関係かどうかはとりあえず置いといて，単に二つの変数（変化するもの）の関係を調べることがよくあります。このような関係を「相関関係」といいます。相関関係のパターンにはいくつかあるので，そのパターンを見てみましょう。

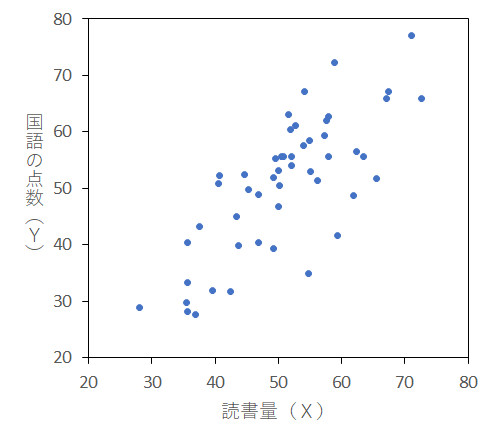
下の図は，「正の相関」関係を表すグラフ（相関図，相関プロット）です。ダミーで作ったデータですが（本当のデータではありません），50人の人について読書量と国語の点数を調べて，それをＸ軸とＹ軸に目盛りをとってグラフにしたと想像してください。このデータを見ると「読書量の多い人ほど国語の点数が高い」という特徴が見られます（点の集まりが右上がり型になっています）。これを，正（プラス）の相関といいます。この例では，読書量の多さが原因となって，国語の点数が結果として上昇したという因果関係の真偽はわかりません。国語の学力が高い人ほど難しい言葉をたくさん知っていますから（語彙が多い），難解な本も楽しめるかもしれません。だから結果として読書量が多くなると考えることもできます。どちらが原因でどちらが結果というのは，必ずしもわからないことは多いのです。それが相関関係です。

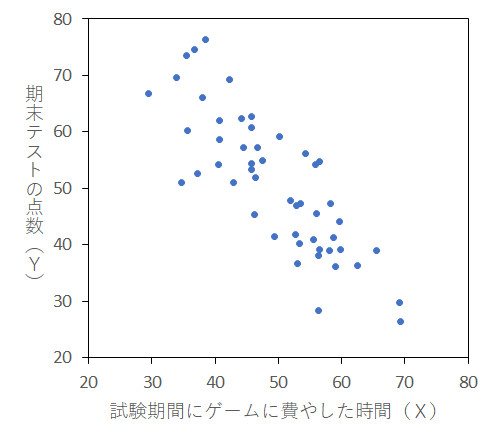
次の例は「負の相関」の例です。正の相関とは逆で，一方の変数が大きくなると，もう一方の変数は小さくなる傾向があります（正の相関とは違って，点の集まりが右下がり型になっています）。これも，必ずしもゲームをしたから期末テストの成績が悪かったという解釈しかできないわけではありません。勉強がわからないので，期末テスト前なのにモチベーションがわかない。だから，勉強しないでゲームに逃げちゃったのかもしれないのですね。

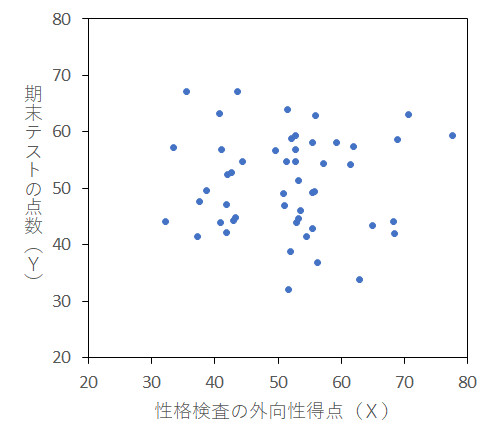
ちなみに，２つの変数の間に特に目立った関係性が存在しないときは，下のような相関図になります。一定の相関関係が見られないこのような状態を無相関と言います。

心理学に限らず，２つの変数の間に相関関係があるかどうかを調べるのは非常によくやる研究手法です。２つの変数が数値的なものであれば，下の式を用いてピアソンの相関係数（r）を算出することで，相関の強さを数値的に求めることができます（具体的な計算方法などは後期の「心理学統計法」という授業で習います）。相関係数である r の値は，正の相関はプラス，負の相関はマイナスで，相関の関係性が強いほど絶対値が１に近くなり，弱いほど０に近くなります。ちなみに，上にグラフで示した正の相関は r = 0.8，負の相関は r = -0.8，無相関は r = 0.0 のものです。

ピアソンの相関係数を求める式

でも，相関関係があることがすなわち因果関係を示すものでないことは，重々承知しておかなければなりません。例えば，疑似相関（偽相関）といって，例えば，第３の変数が介在することで２つの変数の間に偽の相関がみられる場合があります。

よく使われる例として，「アイスクリームの売り上げ」と「水難事故の件数」の間には正の相関がみられますが，これはどちらも「気温の上昇」という共通の原因が影響しているからです（アイスクリームも水難事故も夏に増えますから）。また，昔よく「育毛シャンプーを使う人は禿げる」という噂があったりしましたが，これは，「薄毛に悩んでいる人が育毛シャンプーをよく使う傾向にある」とことを逆の因果関係に取り違えたものということになります。

ちなみに，このような疑似相関（偽相関）にはいろいろジョークのネタになるものもあって，下のグラフは英語でその名も「偽相関（spurious correlations）」というサイトに掲載されている「ミスアメリカに選ばれた女性の年齢」と「熱湯や蒸気をかけるといった（狂気的な）殺人事件の件数」ですが，r = 0.87という高い正の相関となっています (^^;)。

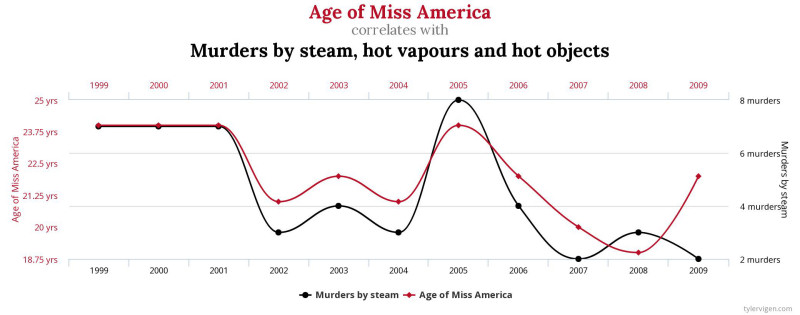
もちろんこの関係を信じる人はいないでしょうが（だからジョークになる），血液型性格検査のように，性格という曖昧なものになると，まったく根拠のないものなのに多くの人が（しかも日本という比較的高度な文明と教育をもつ先進国の国民が）広く信じてしまうという問題が生じてしまうのです。心のもつ特性というものはどうしても曖昧なものなので，心理学を学ぶ我々は，このような間違いを犯さないように気をつけなければいけません。（加筆しました。）

確認テストに答える　← 受講生は必ず答えてください。